MIA > Biblioteca > Albert Einstein > Novidades
Em que medida a teoria da relatividade especial é apoiada pela experiência? Esta pergunta não é facilmente respondida pela razão já mencionada em conexão com o experimento fundamental de Fizeau. A teoria da relatividade especial cristalizou-se a partir da teoria de Maxwell-Lorentz dos fenômenos eletromagnéticos. Assim, todos os fatos da experiência que sustentam a teoria eletromagnética também apoiam a teoria da relatividade. Como sendo de particular importância, menciono aqui o fato de que a teoria da relatividade nos permite prever os efeitos produzidos sobre a luz que nos chega a partir das estrelas fixas. Estes resultados são obtidos de uma maneira extremamente simples, e os efeitos indicados, que são devidos ao movimento relativo da Terra com referência a essas estrelas fixas, são encontrados de acordo com a experiência. Referimo-nos ao movimento anual da posição aparente das estrelas fixas resultante do movimento da Terra em torno do Sol (translação), e à influência dos componentes radiais dos movimentos relativos das estrelas fixas em relação à Terra sobre a cor da luz que nos chega a partir delas. Este último efeito manifesta-se num ligeiro deslocamento das linhas espectrais da luz que nos é transmitida a partir de uma estrela fixa, em comparação com a posição das mesmas linhas espectrais quando são produzidas por uma fonte terrestre de luz (efeito Doppler). Os argumentos experimentais a favor da teoria de Maxwell-Lorentz, que são ao mesmo tempo argumentos a favor da teoria da relatividade, são muito numerosos para serem expostos aqui. Na realidade, eles limitam as possibilidades teóricas a tal ponto, que nenhuma outra teoria além da de Maxwell e Lorentz foi capaz de se manter quando testada pela experiência.
Mas há duas classes de fatos experimentais até agora obtidos que podem ser representados na teoria de Maxwell-Lorentz apenas pela introdução de uma hipótese auxiliar, que em si mesma – isto é, sem fazer uso da teoria da relatividade – parece estranha.
Sabe-se que os raios catódicos e os chamados raios β emitidos por substâncias radioativas consistem em partículas (elétrons) negativamente eletrificadas de inércia muito pequena e grande velocidade. Examinando a deflexão desses raios sob a influência de campos elétricos e magnéticos, podemos estudar a lei do movimento dessas partículas com muita precisão.
No tratamento teórico desses elétrons, nos deparamos com a dificuldade de que a teoria eletrodinâmica de si mesma seja incapaz de dar conta de sua natureza. Pois, como as massas elétricas de um signo se repelem, as massas elétricas negativas que constituem o elétron seriam necessariamente dispersas sob a influência de suas repulsões mútuas, a menos que haja forças de outro tipo operando entre elas, cuja natureza até agora permaneceu obscura para nós.(1) Se assumirmos agora que as distâncias relativas entre as massas elétricas que constituem o elétron permanecem inalteradas durante o movimento do elétron (conexão rígida no sentido da mecânica clássica), chegamos a uma lei de movimento do elétron que não concorda com a experiência. Guiado por pontos de vista puramente formais, H. A. Lorentz foi o primeiro a introduzir a hipótese de que a forma do elétron experimenta uma contração na direção do movimento em consequência desse movimento. o comprimento contratado sendo proporcional à expressão
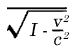
Esta, hipótese, que não é justificável por nenhum fato eletrodinâmico, nos fornece então essa lei particular do movimento que foi confirmada com grande precisão nos últimos anos.
A teoria da relatividade conduz à mesma lei do movimento, sem exigir qualquer hipótese especial quanto à estrutura e ao comportamento do elétron. Chegamos a uma conclusão semelhante na Seção 13 em conexão com o experimento de Fizeau, cujo resultado é previsto pela teoria da relatividade sem a necessidade de recorrer a hipóteses quanto à natureza física do líquido.
A segunda classe de fatos a que aludimos refere-se à questão de saber se o movimento da Terra no espaço pode ou não ser perceptível em experimentos terrestres. Já observamos na secção 5 que todas as tentativas desta natureza conduziram a um resultado negativo. Antes que a teoria da relatividade fosse apresentada, era difícil se reconciliar com esse resultado negativo, por razões ora a serem discutidas. Os preconceitos herdados sobre o tempo e o espaço não permitiram que surgissem dúvidas quanto à importância primordial da transformada de Galileu para a passagem de um corpo de referência para outro. Agora supondo que as equações de Maxwell-Lorentz valem para um corpo-referência K, então descobrimos que elas não valem para um corpo-referência K 1 movendo-se uniformemente em relação a K, se assumirmos que as relações da transformada de Galileu existem entre as coordenadas de K e K1. Assim, parece que, de todos os sistemas de coordenadas de Galileu, um (K) correspondente a um estado particular de movimento é fisicamente único. Este resultado foi interpretado fisicamente considerando K como em repouso em relação a um éter hipotético do espaço. Por outro lado, todos os sistemas de coordenadas K 1 que se movem relativamente a K devem ser considerados como em movimento em relação ao éter. A este movimento de K 1 contra o éter ("æther-drift " em relação a K 1) foram atribuídas as leis mais complicadas que deveriam valer em relação a K 1. Estritamente falando, tal éter-deriva também deve ser assumida em relação à Terra, e por muito tempo os esforços dos físicos foram dedicados a tentativas de detectar a existência de uma éter-deriva na superfície da Terra.
Em uma das tentativas mais notáveis, Michelson concebeu um método que parece dever ser decisivo. Imagine dois espelhos tão dispostos em um corpo rígido que as superfícies refletivas se enfrentam. Um raio de luz requer um tempo T perfeitamente definido para passar de um espelho para o outro e vice-versa, se todo o sistema estiver em repouso em relação ao éter. Verifica-se, por cálculo, no entanto, que um tempo ligeiramente diferente T1 é necessário para este processo, se o corpo, juntamente com os espelhos, estiver se movendo relativamente ao éter. E ainda outro ponto: é mostrado pelo cálculo que, para uma dada velocidade v com referência ao éter, desta vez T1 é diferente quando o corpo está se movendo perpendicularmente aos planos dos espelhos daquela resultante quando o movimento é paralelo a esses planos. Embora a diferença estimada entre esses dois tempos seja extremamente pequena, Michelson e Morley realizaram um experimento envolvendo interferência no qual essa diferença deveria ter sido claramente detectável. Mas o experimento deu um resultado negativo – um fato que deixou os físicos muito perplexos. Lorentz e FitzGerald resgataram a teoria dessa dificuldade assumindo que o movimento do corpo em relação ao éter produz uma contração do corpo na direção do movimento, sendo a quantidade de contração apenas suficiente para compensar a diferença no tempo mencionada acima. A comparação com a discussão da Seção 11 mostra que, também do ponto de vista da teoria da relatividade, essa solução da dificuldade foi a correta. Mas, com base na teoria da relatividade, o método de interpretação é incomparavelmente mais satisfatório. De acordo com esta teoria, não existe um sistema de coordenação " especialmente favorecido " (único) para ocasionar a introdução da éter-ideia, e, portanto, não pode haver æther-drift, nem qualquer experimento com o qual demonstrá-la. Aqui, a contração dos corpos em movimento decorre dos dois princípios fundamentais da teoria, sem a introdução de hipóteses particulares; e como fator primordial envolvido nessa contração encontramos, não o movimento em si, ao qual não podemos atribuir qualquer significado, mas o movimento em relação ao corpo de referência escolhido no caso particular em questão. Assim, para um sistema coordenado que se move com a Terra, o sistema de espelhos de Michelson e Morley não é encurtado, mas é encurtado para um sistema coordenado que está em repouso relativamente ao Sol.
Nota de rodapé:
(1) A teoria geral da relatividade torna provável que as massas elétricas de um elétron sejam mantidas juntas por forças gravitacionais. (retornar ao texto)