MIA > Biblioteca > Albert Einstein > Novidades
<<< Índice
Relatividade: A Teoria Restrita e Geral
Albert Einstein
13 - Teorema da Adição de Velocidades. A Experiência de Fizeau
Ora, na prática, só podemos mover relógios e réguas de medição com velocidades pequenas comparadas com a velocidade da luz; portanto, dificilmente seremos capazes de comparar diretamente os resultados da seção anterior com a realidade. Mas, por outro lado, estes resultados devem parecer-vos muito singulares, e por essa razão tirarei agora outra conclusão da teoria, uma conclusão que pode ser facilmente derivada das considerações anteriores, e que foi elegantemente confirmada por experimentar.
Na Seção 6 derivamos o teorema da adição de velocidades em uma direção na forma que também resulta das hipóteses da mecânica clássica. Este teorema também pode ser deduzido facilmente da transformação de Galilei (Seção 11). No lugar do homem caminhando dentro da carruagem, introduzimos um ponto que se move em relação ao sistema de coordenadas K1 de acordo com a equação
x1 = peso1
Por meio da primeira e da quarta equações da transformação de Galileu podemos expressar x1 e t1 em termos de x e t, e obtemos então
x = (v + w)t
Esta equação nada mais expressa do que a lei do movimento do ponto em relação ao sistema K (do homem em relação ao aterro). Denotamos esta velocidade pelo símbolo W e obtemos então, como na Seção 6,
W=v+w A)
Mas também podemos levar a cabo esta consideração com base na teoria da relatividade. Na equação
x1 = peso1 B)
devemos então expressar x1 e t1 em termos de x e t, fazendo uso da primeira e quarta equações da transformação de Lorentz. Em vez da equação (A), obtemos então a equação
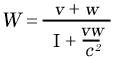
que corresponde ao teorema da soma de velocidades em uma direção conforme a teoria da relatividade. A indagação que surge é quando qual destes dois teoremas é superior segundo a experiências. Neste ponto somos esclarecidos pela experência mais importante do físico brilhante Fizeau realizada há mais de meio século atrás, e que foi repetida desde então pelos melhores físicos experimentais, desta forma não há dúvidas quanto ao resultado. A experiência diz respeito ao seguinte problema. A luz atravessa um líquido imóvel com uma velocidade particular w. Quanto rapidamente ela atravessa o cano na direção da seta o cano T (veja o seguinte diagrama, fig. 3) quando o líquido acima mencionado percorre o cano com a velocidade v ?
De acordo com o princípio da relatividade teremos certamente de tomar como garantida a propagação da luz sempre acontece com a mesma velocidade w relativa ao líquido, embora o movimento posterior de movimento com referência a outros corpos ou não. A velocidade da luz relativa ao líquido e a velocidade posterior relativa ao cano são assim conhecidas, e precisamos da velocidade da luz relativa ao cano.
Está claro que temos diante de nós o problema da seção 6 novamente diante de nós. O cano toma parte do aterramento da ferrovia ou do sistema de coordenada do sistema K, o líquido toma parte do carro ou do sistema de coordenadas K1, e finalmente, a luz toma parte do

homem andando através do carro, ou do ponto de movimento na presente secção. Se nós expressarmos a velocidade da luz relativa ao cano por W, então isto é dado pela equação (A) ou (B), segundo a transformada de Galileu ou a de Lorentz correspondente aos fatos. A Experiência(1) decide em favor da equação (B) derivada da teoria da relatividade, e a concordância é, realmente, muito exata. Segundo as medidas excelentes e mais recentes de Zeeman, a influência da velocidade de fluxo v na propagação da luz é representada pela fórmula (B) com a margem de um por cento.
Contudo devemos prestar atenção de que a teoria deste fenômeno foi dada por H. A. Lorentz muito antes do estabelecimento da teoria da relatividade. Esta teoria foi simplesmente de natureza eletrodinâmica, e foi obtida pelo uso particular da hipótese particular da estrutura eletromagnética da matéria. Esta circunstância, entretanto , não diminui minimamente a conclusão afirmativa da experiência como uma prova crucial em favor da teoria da relatividade, para a eletrodinâmica de Maxwell-Lorentz, na qual a teoria original foi baseada, sem argumento contrário que se oponha à teoria da relatividade. Antes disso os recentes tempos tem sido desenvolvida da eletrodinâmica como uma combinação extraordinariamente simples e uma generalização de hipóteses, certamente independente uma da outra, na qual a eletrodinâmica foi construída.
continua >>>
Início da página
Nota de rodapé:
(1) Fizeau encontrou 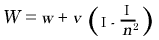 , onde
, onde 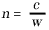 é o índice de refração do líquido. Por outro lado, devido à pequenez de
é o índice de refração do líquido. Por outro lado, devido à pequenez de 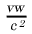 em comparação com I, podemos substituir (B) em primeiro lugar por
em comparação com I, podemos substituir (B) em primeiro lugar por 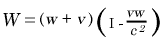 , , ou na mesma ordem de aproximação por
, , ou na mesma ordem de aproximação por 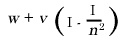 , o que concorda com o resultado de Fizeau. (retornar ao texto)
, o que concorda com o resultado de Fizeau. (retornar ao texto)
Inclusão: 03/11/2023
Última atualização: 06/11/2023
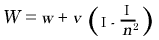 , onde
, onde 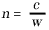 é o índice de refração do líquido. Por outro lado, devido à pequenez de
é o índice de refração do líquido. Por outro lado, devido à pequenez de 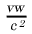 em comparação com I, podemos substituir (B) em primeiro lugar por
em comparação com I, podemos substituir (B) em primeiro lugar por 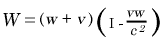 , , ou na mesma ordem de aproximação por
, , ou na mesma ordem de aproximação por 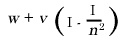 , o que concorda com o resultado de Fizeau. (retornar ao texto)
, o que concorda com o resultado de Fizeau. (retornar ao texto)