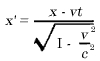
MIA > Biblioteca > Albert Einstein > Novidades
Os resultados das três últimas seções mostram que a aparente incompatibilidade da lei de propagação da luz com o princípio da relatividade (Seção 7) foi obtida por meio de uma consideração que emprestou duas hipóteses injustificáveis para a mecânica clássica; estas são as seguintes:
(1) O intervalo de tempo (tempo) entre dois eventos é independente da condição de movimento do corpo de referência.
(2) O intervalo de espaço (distância) entre dois pontos de um corpo rígido é independente da condição de movimento do corpo de referência.
Se abandonarmos essas hipóteses, o dilema da Seção 7 desaparecerá, porque o teorema da adição de velocidades derivado na Seção 6 se torna inválido. A possibilidade apresenta-se que a lei de propagação da luz no vácuo pode ser compatível com o princípio da relatividade, e surge a pergunta: como modificar as considerações da Seção 6 , a fim de remover o aparente desacordo entre esses dois princípios resultados da experiência? Esta questão leva a uma questão geral. Na discussão da Seção 6 temos a ver com lugares e horários relativos ao trem e ao aterro. O quanto devemos encontrar o local e a hora de um evento em relação ao trem, quando conhecemos o local e hora do evento em relação ao aterro da ferrovia? Existe uma resposta imaginável a esta questão de tal natureza que a lei da transmissão da luz no vácuo não contradiga o princípio da relatividade? Em outras palavras: podemos conceber uma relação entre o local e a hora dos eventos individuais relativos a ambos os eventos de referência, de modo que todo raio de luz possui a velocidade de transmissão c em relação ao aterro e em relação ao trem? Essa pergunta leva a uma resposta positiva bastante definida e a uma lei da transformada perfeitamente definida para as magnitudes espaço-tempo de um evento quando passando de um corpo de referência para outro.
Antes de lidarmos com isso, apresentaremos a seguinte consideração incidental. Até o presente, consideramos apenas os eventos ocorridos ao longo do aterro, que haviam matematicamente assumido a função de uma linha reta. Da maneira indicada na Seção 2 podemos imaginar esse corpo de referência suplementado lateralmente e verticalmente por meio de uma estrutura de hastes, para que um evento que ocorre em qualquer lugar possa ser localizado com referência a esta estrutura. Da mesma forma, podemos imaginar o trem viajando com a velocidade v para ser contínua em todo o conjunto de espaço, para que cada evento, não importa o quanto distante, também pode ser localizado com relação ao segundo quadro.
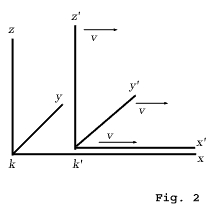
Sem cometer qualquer erro fundamental, podemos desconsiderar o fato de que, na realidade, essas estruturas interfeririam continuamente devido à impenetrabilidade dos corpos sólidos. Em toda essa estrutura, nós imaginamos três superfícies perpendiculares a cada outro marcado e designado como "planos de coordenadas" (" sistema de coordenadas"). Um sistema de coordenadas K corresponde então ao aterro e um sistema de coordenadas K ' para o trem. Um evento, onde quer que tenha ocorrido, seria fixado no espaço em relação a K pelas três perpendiculares x, y, z nos planos coordenados e, em relação ao tempo, por um valor de tempo t. Em relação a K 1 , o mesmo evento seria corrigido em relação ao espaço e ao tempo pelos valores correspondentes x 1 , y 1 , z 1 , t 1 , que obviamente não são idênticos a x, y, z, t. Já foi estabelecido em detalhes como essas magnitudes devem ser consideradas como resultados de medições físicas.
Obviamente, nosso problema pode ser formulado exatamente da seguinte maneira. O que são os valores x 1 , y 1 , z 1 , t 1 , de um evento em relação a K 1 , quando as magnitudes x, y, z, t, do mesmo evento em relação a K é dado? As relações devem ser escolhidas de maneira que a lei da transmissão de luz in vácuo é satisfeita por um e o mesmo raio de luz (e, é claro, para cada raio) em relação a K e K 1 . Para a orientação relativa no espaço dos sistemas de coordenadas indicados no diagrama ( Fig. 2 ), esse problema é resolvido por meio das equações:
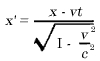
y 1 = y
z 1 = z
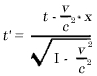
Esse sistema de equações é conhecido como "transformada de Lorentz".(1) Se, no lugar da lei da transmissão da luz, tivéssemos como base as tácitas suposições da mecânica mais antiga quanto ao caráter absoluto de tempos e comprimentos, em vez do acima, deveríamos ter obtido as seguintes equações:
x 1 = x - vt
y 1 = y
z 1 = z
t 1 = t
Este sistema de equações é frequentemente denominado "transformada de Galileu". Esta última transformada pode ser obtida a partir da transformada de Lorentz, substituindo o infinitamente grande valor para a velocidade da luz c na última transformada.
Ajudados pela ilustração a seguir, podemos ver facilmente que, de acordo com a transformada de Lorentz, a lei da transmissão da luz no vácuo é satisfeita tanto pelo corpo de referência K e para o corpo de referência K 1 . Um sinal de luz é enviado ao longo do eixo x positivo, e esse estímulo luminoso avança de acordo com a equação
x = ct,
ou seja, com a velocidade c. De acordo com as equações da transformada de Lorentz, essa relação simples entre x e t envolve uma relação entre x 1 e t 1 . De fato, se nós substituímos por x o valor ct na primeira e quarta equações da transformada de Lorentz, nós obtemos:
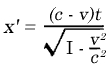
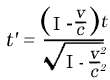
a partir do qual, por divisão, a expressão
x1 = ct1
segue imediatamente. Se referido ao sistema K 1 , a propagação da luz ocorre de acordo com esta equação. Vemos, assim, que a velocidade de transmissão em relação à corpo de referência K 1 também é igual a c. O mesmo resultado é obtido para os raios de luz avançando em qualquer outra direção. Isso não é surpreendente, uma vez que as equações da transformada de Lorentz foi derivada de acordo com esse ponto de vista.
Notas de rodapé:
(1) Uma simples derivação da transformada de Lorentz é dada no apêndice I. (retornar ao texto)