MIA > Biblioteca > Albert Einstein > Novidades
Coloque uma barra de medição no eixo x 1 de K 1 de tal maneira que um fim (o começo) coincida com o ponto x 1 = 0 enquanto a outra extremidade (a extremidade da barra) coincida com o ponto x 1 = I. Qual é o comprimento da barra de medição em relação ao sistema K? Para aprender isso, precisamos apenas perguntar onde estão o começo e o fim da barra com relação ao sistema K em um determinado momento t do sistema K. Por meio da primeira equação da transformada de Lorentz, os valores desses dois pontos no momento t = 0 podem ser mostrados como sendo
a distância entre os pontos 
.
Mas a haste do medidor está se movendo com a velocidade v em relação a K. Segue-se, portanto, que o comprimento de uma barra rígida, movendo-se na direção de seu comprimento com uma velocidade v, é 
de um metro.
A barra rígida é, portanto, mais curta quando em movimento do que quando em repouso, e quanto mais rapidamente em movimento, menor é a haste. Para a velocidade v = c, deveríamos ter 
, e, para velocidades ainda maiores, a raiz quadrada se torna imaginária. A partir disso, concluímos que, na teoria da relatividade, a velocidade c desempenha o papel de uma velocidade limitante, que pode nem ser alcançada nem excedido por nenhum corpo real.
Obviamente, esse recurso da velocidade c como velocidade limitadora também segue claramente das equações da transformada de Lorentz, pois estas se tornam sem sentido se escolhermos valores de v maior que c.
Se, pelo contrário, tivéssemos considerado uma barra de medição em repouso no eixo x em relação a K, então deveríamos ter descoberto que o comprimento da barra como julgado em K 1 teria sido 
; isso está de acordo com o princípio da relatividade que forma a base de nossas considerações.
A priori , é bastante claro que devemos ser capazes de aprender algo sobre o comportamento físico das barras de medição e relógios das equações de transformada, para as magnitudes z, y, x, t nada mais são do que os resultados das medições obtidas por meio de hastes e relógios. Se tivéssemos baseado nossas considerações na transformada de Galileu, não deveríamos ter obtido uma contração da haste como consequência de seu movimento.
Vamos agora considerar um relógio de segundos permanentemente situado na origem (x 1 = 0) de K 1 . t 1 = 0 e t 1 = I são dois pulsos sucessivos deste relógio. A primeira e quarta equações da transformada de Lorentz dá para esses dois pulsos:
e
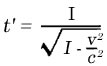
Como julgado por K, o relógio está se movendo com a velocidade v; julgado a partir deste corpo de referência, o tempo decorrido entre dois movimentos do relógio não é um segundo, mas
segundos, ou seja , um tempo um pouco maior. Como consequência de seu movimento, o relógio vai mais lentamente do que quando em repouso. Aqui também a velocidade c desempenha o papel de uma limitação de velocidade inatingível.