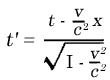
MIA > Biblioteca > Albert Einstein > Novidades
O não-matemático é tomado por um misterioso estremecimento quando ouve de coisas como "quatro" dimensões, por um sentimento não muito diferente daquele despertado por pensamentos do oculto. E, no entanto, não há mais uma declaração comum do que o mundo em que vivemos é um contínuo de espaço-tempo de quatro dimensões.
O espaço é um contínuo tridimensional. Com isso queremos dizer que é possível descrever a posição de um ponto (em repouso) por meio de três números (coordenados) x, y, z, e que há um número indefinido de pontos na vizinhança deste, cuja posição pode ser descrita por coordenadas como x1, y1, z1, que podem ser tão próximas quanto escolhemos para os respectivos valores das coordenadas x, y, z, do primeiro ponto. Em virtude da última propriedade, falamos de um "continuum", e devido ao fato de que há três coordenadas, falamos disso como sendo "três dimensões".
Da mesma forma, o mundo dos fenômenos físicos que foi brevemente chamado de "mundo" por Minkowski é naturalmente quadridimensional no sentido do espaço-tempo. Pois é composto de eventos individuais, cada um dos quais é descrito por quatro números, ou seja, três coordenadas espaciais x, y, z, e uma coordenada de tempo, o valor do tempo t. O "mundo" é, neste sentido, também um continuum; para cada evento há tantos eventos "pesados" (realizados ou pelo menos pensáveis) como nos preocupamos em escolher, as coordenadas x1, y1, z1, t1 das quais diferem por uma quantidade indefinidamente pequena daquelas do evento x, y, z, originalmente considerado. Que não estamos acostumados a considerar o mundo nesse sentido como um contínuo quadridimensional é devido ao fato de que, na física, antes do advento da teoria da relatividade, o tempo desempenhou um papel diferente e mais independente, em comparação com as coordenadas do espaço. É por isso que temos o hábito de tratar o tempo como um continuum independente. De fato, de acordo com a mecânica clássica, o tempo é absoluto, ou seja, é independente da posição e da condição de movimento do sistema de coordenadas. Vemos isso expresso na última equação da transformada de Galileu (t1 = t)
O modo de consideração quadridimensional do "mundo" é natural na teoria da relatividade, uma vez que, de acordo com essa teoria, o tempo é roubado de sua independência. Isso é mostrado pela quarta equação da transformada de Lorentz:
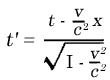
Além disso, de acordo com esta equação, a diferença de tempo Δt1 de dois eventos em relação ao K1 não desaparece em geral, mesmo quando a diferença de tempo Δt1 dos mesmos eventos com referência a K desaparece. Pura "distância espacial" de dois eventos em relação a K resulta em "tempo-distância" dos mesmos eventos em relação a K. Mas a descoberta de Minkowski, que era importante para o desenvolvimento formal da teoria da relatividade, não está aqui. É encontrado em vez disso O fato de seu reconhecimento de que o quadridimensional espaço-tempo contínuo da teoria da relatividade, em sua As propriedades formais mais essenciais, mostram uma relação com o continuum tridimensional de Espaço geométrico euclidiano(1). A fim de dar devido proeminência com esta relação, no entanto, devemos substituir o tempo habitual coordenado t por um imaginário magnitude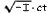 
proporcional a ele. Sob estes as condições, as leis naturais que satisfazem as exigências de a teoria (especial) da relatividade assume matemática formas, em que o tempo coordenado joga exatamente o o mesmo papel das três coordenadas espaciais. Formalmente, estas quatro coordenadas correspondem exatamente às três coordenadas na geometria euclidiana. Tem que ser claro até mesmo para o não-matemático que, como consequência deste complemento puramente formal ao nosso conhecimento, a teoria ganhou clareza em forte medida.
Essas observações inadequadas podem dar ao leitor apenas uma vaga noção da importante ideia contribuída por Minkowski. Sem ele, a teoria geral da relatividade, da qual as ideias fundamentais são desenvolvidas nas páginas seguintes, talvez não teria se aproximado do que suas roupas longas. O trabalho de Minkowski é, sem dúvida, difícil de acessar qualquer pessoa inexperiente em matemática, mas como não é necessário ter uma compreensão muito exata deste trabalho, a fim de compreender as ideias fundamentais da teoria da relatividade especial ou geral, vou deixá-la aqui no momento, e reverterei a ela apenas no final da Parte II.
Nota de rodapé:
(1) Cf. O debate um pouco mais detalhado no Apêndice II. (retornar ao texto)